神经网络

神经网络#

神经网络的基本计算单元是神经元（或节点）。神经元接收来自其他神经元或外部数据源的多个输入信号。每个输入信号都有一个关联的权重代表该输入的重要性。

线性回归#

线性回归通过学习一个线性函数来对输入特征和输出结果之间的关系进行建模。

一个预测值 \(\hat{y}\) 是通过以下方式计算的：

\[ \hat{y} = w_1 x_1 + w_2 x_2 + ... + w_n x_n + b = \mathbf{W}^T \mathbf{X} + b \]

其中：

  • \(\mathbf{X} = (x_1, x_2, ..., x_n)\) 是输入特征向量。

  • \(\mathbf{W} = (w_1, w_2, ..., w_n)\) 是模型的权重，表示每个特征的重要性。

  • \(b\) 是偏置项。

学习过程的目标就是找到最优的权重 \(\mathbf{W}\) 和偏置 \(b\)。

Softmax回归#

Softmax回归是一个分类问题，分类预测一个离散类别（输出的个数是类别的个数）。Softmax的作用是将一个包含任意实数值的向量转换为一个概率分布。每个元素的值都在0-1之间并且总和为1，使得模型的输出可以直接解释为输入样本属于每一个类别的概率，用于多分类问题的输出层。

\[ Softmax(x_i) = \frac{e^{x_i}}{\sum_{j=1}^{n}e^{x_j}}, \quad i=1,2,...,n \]

多层感知机#

感知机是 20 世纪 50 年代末期被提出的神经网络最基础、最简单的原型。感知机是一个二分类模型，使用了一个简单的阶跃函数作为输出函数，感知机只能学习线性可分的数据模式。

\( \sigma(x)= \begin{cases} 1 & \text{if } x > 0 \\ 0 & \text{otherwise} \end{cases} \)

多层感知机通过在输入层和输出层之间加入一个或多个隐藏层，并使用非线性的激活函数，能够处理和学习非线性模式，广泛应用于分类、回归等任务。

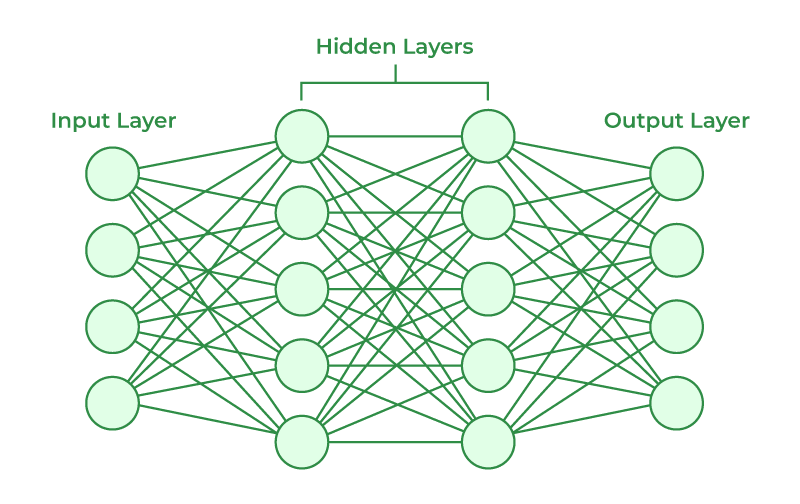
神经网络结构

神经网络由输入层、隐藏层和输出层组成。输入层接收原始数据。该层的神经元数量通常等于数据特征的数量。隐藏层位于输入层和输出层之间，负责提取数据中的各种特征。一个神经网络可以没有隐藏层（如逻辑回归），也可以有一个或多个隐藏层。拥有多个隐藏层的网络通常被称为深度神经网络。输出层产生最终的预测结果，该层的神经元数量和激活函数取决于具体任务。

激活函数#

激活函数被应用于神经元的输出为其引入非线性。如果没有非线性激活函数，无论神经网络有多少层，本质上都只是一个线性模型，无法学习和表示复杂的数据模式。

  • Sigmoid 函数将任意实数输入压缩到 (0, 1) 的范围内，可以被解释为概率，常用于二分类问题的输出层或作为门控机制。

    \[ f(x) = \frac{1}{1 + e^{-x}} \]

    但是当输入值非常大或非常小时，函数的梯度会趋近于0，在反向传播过程中，会导致深层网络的梯度信号变得非常微弱，使得网络难以训练。

  • Tanh (双曲正切) 函数可以看作是 Sigmoid 函数的一个缩放和移位版本，它将输入压缩到 (-1, 1) 的范围内。通常比 Sigmoid 函数有更好的性能，收敛速度更快，但仍然存在梯度消失的问题。

    \[ f(x) = \tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} \]

  • ReLU 是目前在深度学习的隐藏层中最常用的激活函数，只涉及一个简单的阈值操作。

    \[ f(x) = \max(0, x) \]

    当输入为正数时，其梯度恒为 1，这使得梯度能够很好地在网络中传播。但是，如果一个神经元的输入在训练过程中持续为负，那么它的梯度将永远为0，导致该神经元的权重无法再被更新。

  • Leaky ReLU 是对 ReLU 的改进，它允许在输入为负时也有一个小的、非零的梯度。\(\alpha\) 是一个很小的常数（如 0.01）。

    \[\begin{split} f(x) = \begin{cases} x & \text{if } x > 0 \\ \alpha x & \text{if } x \le 0 \end{cases} \end{split}\]
Contents